2つのベクトル間の角度を見つける方法：12ステップ（写真付き） - チップ

コンテンツ

手順
助言

あなたが数学者またはグラフィックプログラマーである場合、おそらく2つの与えられたベクトル間の角度を見つける必要があります。この記事では、wikiHowがまさにそれを行う方法を示しています。

手順

パート1/2：2つのベクトル間の角度を見つける

ベクトル定義。 あなたが持っている2つのベクトルに関するすべての情報を書き留めてください。それらの寸法座標（コンポーネントとも呼ばれる）の指定されたパラメーターのみがあるとします。ベクトルの長さ（大きさ）がすでにわかっている場合は、以下の手順のいくつかをスキップできます。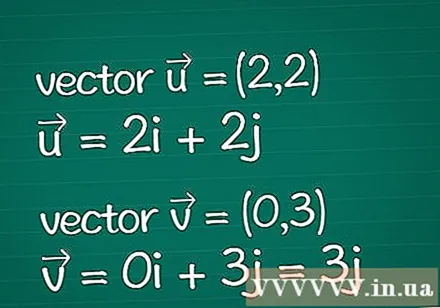
- 例：2次元ベクトル=（2,2）および2次元ベクトル=（0,3）。それらは= 2と書くこともできます私 + 2j および= 0私 + 3j = 3j.
- この記事の例では2次元ベクトルが使用されていますが、次の手順は、任意の数の次元を持つベクトルに適用できます。
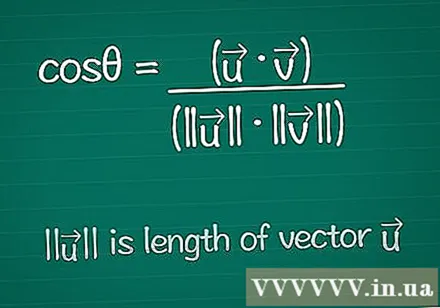
コサイン式を書き留めます。 2つのベクトル間の角度θを見つけるために、その角度の余弦を見つけるための式から始めます。以下でこの式について学ぶか、次のように書き留めてください。
- cosθ=（•）/（|||| ||||）
- |||| 「ベクトルの長さ」を意味します。
- •は2つのベクトルのスカラー積です。これについては以下で説明します。
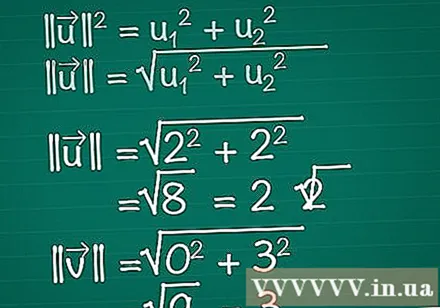
各ベクトルの長さを計算します。 右の三角形がベクトルのx、y成分、およびベクトル自体で構成されていると想像してください。ベクトルは三角形のhypotenuseを形成するため、その長さを見つけるには、Pythagoreanの定理を使用します。実際、この式は、任意の数の次元のベクトルに簡単に拡張できます。
- || u || = u₁ + u₂。ベクトルに3つ以上の要素がある場合は、+ uを追加し続けるだけです。₃ + u₄ +...
- したがって、2次元ベクトルの場合、 || u || =√（u₁ + u₂).
- この例では、|||| =√（2 + 2）=√（8）= 2√2. |||| = √(0 + 3) = √(9) = 3.
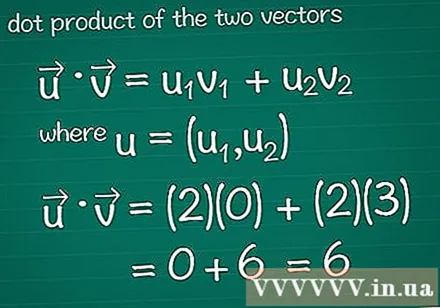
2つのベクトルのスカラー積を計算します。 おそらくあなたはベクトル乗算の方法を学びました。 スカラー この。組成に対するスカラー積を計算するには、各方向の成分を乗算してから、結果全体を合計します。
- グラフィックプログラムについては、さらに読む前にヒントを参照してください。
- 数学で •= u₁v₁ + u₂v₂、ここで、u =（u₁、u₂）。ベクトルに3つ以上の要素がある場合は、+ uを追加するだけです。₃v₃ + u₄v₄...
- この例では、•= u₁v₁ + u₂v₂ = (2)(0) + (2)(3) = 0 + 6 = 6。これは、ベクトルとベクトルのスカラー積です。
結果を式に入れます。 cosθ=（•）/（|||| || ||）であることを忘れないでください。これで、スカラー積と各ベクトルの長さの両方がわかりました。これらを式に入力して、角度の余弦を計算します。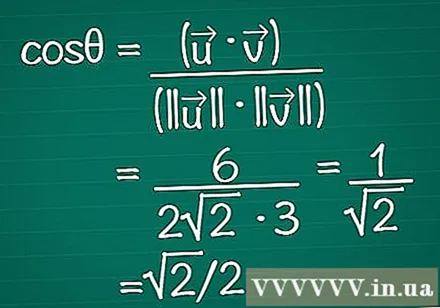
- この例では、cosθ= 6 /（2√2 * 3）= 1 /√2=√2/ 2です。
その余弦に基づいて角度を見つけます。 計算機でarccosまたはcos関数を使用して、既知のcos値からθを見つけることができます。いくつかの結果では、単位円に基づいて角度を見つけることができます。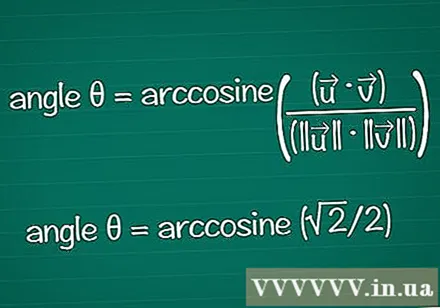
- この例では、cosθ=√2/ 2です。計算機に「arccos（√2/ 2）」と入力して角度を見つけます。または、位置cosθ=√2/ 2で、単位円上の角度θを見つけることができます。これは、 θ = /₄ または45º.
- すべてを組み合わせると、最終的な式は次のようになります。角度θ=アークコサイン（（•）/（|||| || ||））
広告

パート2/2：角度式の決定

式の目的を理解します。 この式は、既存のルールから派生したものではありません。代わりに、スカラー積と2つのベクトル間の角度の定義として形成されます。それでも、それは恣意的な決定ではありませんでした。基本的なジオメトリに戻ると、この式が直感的で有用な定義を提供する理由を理解できます。
- 以下の例では、最も理解しやすく単純な2次元ベクトルを使用しています。 3次元以上のベクトルは、ほぼ同様の一般式で定義された特性を持っています。
コサインの定理を確認します。 辺aと辺bの間、辺cの反対側に角度θがある通常の三角形を考えてみます。コサイン定理は、c = a + b-2abと述べていますcos（θ）。この結果は、基本的なジオメトリから非常に単純に描かれています。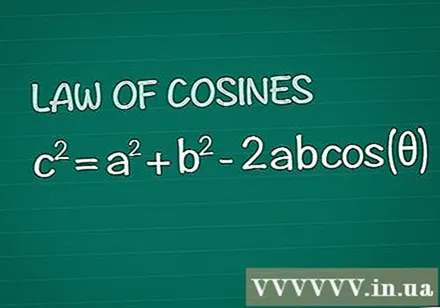
2つのベクトルを接続し、三角形を形成します。 紙に2次元ベクトルのペア、ベクトルとベクトルを描画します。θはそれらの間の角度です。これら2つの間に3番目のベクトルを描画して、三角形を作成します。つまり、+ =のようなベクトルを描画します。ベクトル=-。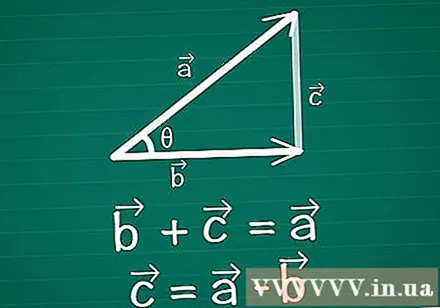
この三角形のコサイン定理を記述します。 「ベクトル三角形」の辺の長さをコサイン定理に代入します。
- ||（a --b）|| = || a || + || b || --2 || a || || b ||cos(θ)
スカラー積で書き直します。 スカラー積は、一方のベクトルのもう一方の画像であることに注意してください。ここでは方向に違いがないため、ベクトルとそれ自体のスカラー積は射影を必要としません。つまり、•= || a ||です。これを使用して、方程式を書き直します。
- （-）•（-）=•+•-2 || a || || b ||cos(θ)
同じ式を正常に書き直しました。 式の左側を展開し、単純化して、角度を見つけるために使用される式を取得します。
- •-•-•+•=•+•-2 || a || || b ||cos(θ)
- -•-•= -2 || a || || b ||cos(θ)
- -2（•）= -2 || a || || b ||cos(θ)
- •= || a || || b ||cos(θ)
広告

助言

値を変更して問題をすばやく解決するには、2次元ベクトルの任意のペアに次の式を使用します：cosθ=（u₁ •v₁ + u₂ •v₂）/（√（u₁ •u₂）•√（v₁ •v₂)).
コンピューターグラフィックスソフトウェアを使用している場合は、ベクトルの長さを気にせずに、ベクトルの寸法だけを気にする必要がある可能性があります。次の手順を使用して、方程式を短くし、プログラムを高速化します。
- 1に等しくなるように各ベクトルを正規化します。これを行うには、ベクトルの各コンポーネントをその長さで除算します。
- 元のベクトルの代わりにスカラーの正規化された積を取得します。
- 長さは1なので、長さの要素を式から除外できます。最後に、得られる角度方程式はarccos（•）です。
コサイン式に基づいて、角度が鋭角であるか鈍角であるかをすばやく判断できます。 cosθ=（•）/（|||| ||||）で開始します。
- 方程式の左辺と右辺は同じ符号（正または負）である必要があります。
- 長さは常に正であるため、cosθはスカラー積と同じ符号を持つ必要があります。
- したがって、積が正の場合、cosθも正になります。私たちは、θ<π/ 2または90ºの単位円の第1象限にいます。見つける角度は鋭い角度です。
- スカラー積が負の場合、cosθは負です。単位円の第2象限にあり、π/ 2 <θ≤πまたは90º<θ≤180ºです。それが刑務所のコーナーです。