著者:
Mark Sanchez
作成日:
28 1月 2021
更新日:
1 J 2024
コンテンツ
有理関数の形式はy = N（x）/ D（x）です。ここで、NとDは多項式です。このような関数を正確にプロットするには、微分計算を含む代数に関する十分な知識が必要です。次の例を考えてみましょう。 y = (2NS - 6NS + 5)/(4NS + 2).
ステップ
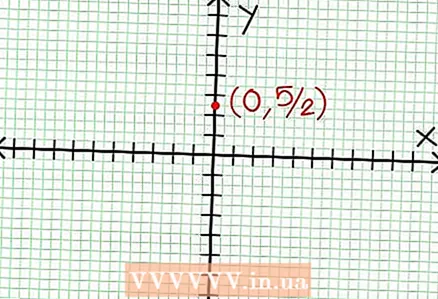1 グラフのy切片を見つけます。 これを行うには、関数にx = 0を代入し、y = 5/2を取得します。したがって、グラフとY軸の交点の座標は（0、5 / 2）になります。この点を座標平面に配置します。 
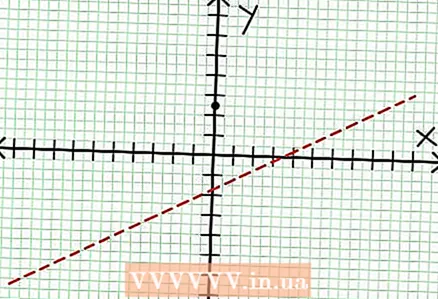2 水平方向の漸近線を見つけます。 分子を分母（列内）で除算して、「x」の値が無限大になる傾向がある「y」の動作を決定します。この例では、分割は次のようになります。 y = (1/2)NS - (7/4) + 17/(8NS + 4）。 「x」の大きな正または負の値の場合17 /（8NS + 4）はゼロになる傾向があり、グラフは関数で与えられる直線に近づきます y = (1/2)NS -（7/4）。点線を使用して、この関数をプロットします。 - 分子の次数が分母の次数よりも小さい場合、分子を分母で割ることはできず、漸近線は関数によって記述されます。 で = 0.
- 分子の次数が分母の次数に等しい場合、漸近線は、最高次数の「x」での係数の比率に等しい水平線です。
- 分子の次数が分母の次数より1大きい場合、漸近線は傾斜した直線であり、その傾きは「x」の係数と最高次数の比率に等しくなります。
- 分子の次数が分母の次数より2、3など大きい場合、値が大きい場合|NS|意味 で 正方形、3次、またはその他の次数の多項式の形で無限大（正または負）になる傾向があります。この場合、ほとんどの場合、分子を分母で割って得られる関数の正確なグラフを作成する必要はありません。
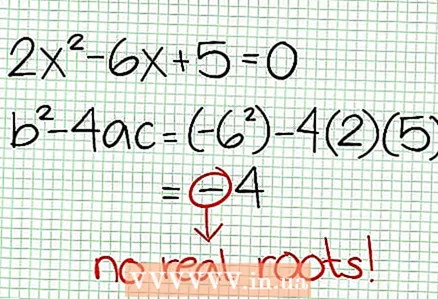3 関数の零点を見つけます。 有理関数は、分子がゼロ、つまりN（NS）= 0。この例では、2NS - 6NS + 5 = 0。この2次方程式の判別式： NS - 4交流 = 6-4 * 2 * 5 = 36-40 = -4。判別式が負であるため、N（NS）、したがってF（NS）本当のルーツはありません。有理関数のグラフはX軸と交差していません。関数にゼロ（根）がある場合は、それらを座標平面に配置します。 
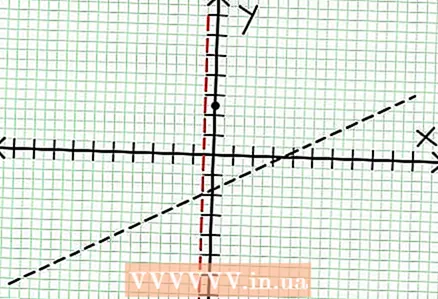4 垂直方向の漸近線を見つけます。 これを行うには、分母をゼロに設定します。この例では、4NS + 2 = 0および NS = -1 / 2。点線を使用して垂直方向の漸近線をプロットします。何らかの価値がある場合 NS NS （NS）= 0およびD（NS）= 0の場合、垂直方向の漸近線が存在するか存在しないかのいずれかです（これはまれなケースですが、覚えておくとよいでしょう）。 
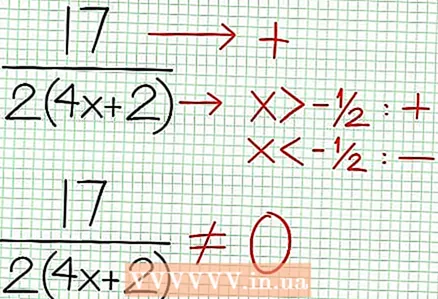5 分母で割った分子の余りを見てください。 それは正、負、またはゼロですか？この例では、余りは17で、正です。分母4NS + 2垂直漸近線の右側に正、左側に負。これは、大きな正の値の有理関数のグラフが NS 上から漸近線に近づき、大きな負の値の場合 NS - 下から。 17 /（8以降NS + 4）がゼロに等しくなることはありません。その場合、この関数のグラフは、関数で指定された直線と交差することはありません。 で = (1/2)NS - (7/4). 
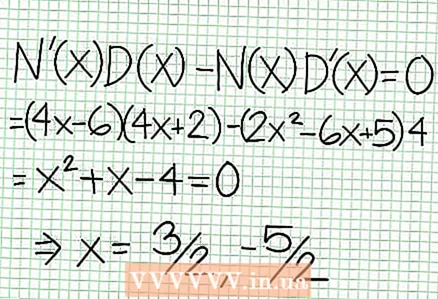6 局所極値を見つけます。 N '（N'（NS） NS （NS） - NS （NS） NS '（NS）= 0。この例では、N ’（NS) = 4NS -6およびD '（NS）= 4. N ’（NS） NS （NS） - NS （NS） NS '（NS) = (4NS - 6)(4NS + 2) - (2NS - 6NS + 5)*4 = NS + NS --4 = 0。この方程式を解くと、次のことがわかります。 NS = 3/2および NS = -5 / 2。 （これらは完全に正確な値ではありませんが、超高精度が必要ない場合に適しています。） 
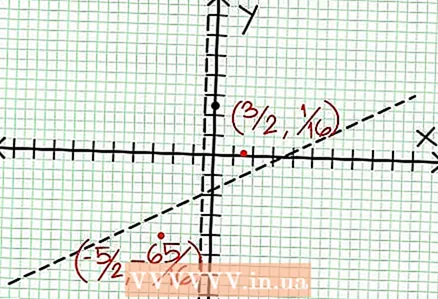7 値を見つける で 各極値に対して。 これを行うには、値を代入します NS 元の有理関数に。この例では、f（3/2）= 1/16およびf（-5/2）=-65/16です。座標平面上の点（3 / 2、1 / 16）と（-5 / 2、-65 / 16）を取っておきます。計算は（前のステップからの）概算値に基づいているため、見つかった最小値と最大値も完全に正確ではありません（ただし、おそらく正確な値に非常に近いです）。 （点（3 / 2、1 / 16）は極小値に非常に近いです。ステップ3から、次のことがわかります。 で 常にポジティブ NS> -1/2、そして小さな値（1/16）が見つかりました。したがって、この場合のエラー値は非常に小さくなります。） 
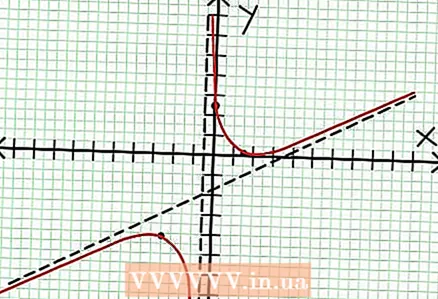8 保留中のポイントを接続し、グラフを漸近線までスムーズに拡張します（グラフが漸近線に近づく正しい方向を忘れないでください）。 グラフがX軸と交差してはならないことに注意してください（手順3を参照）。グラフは、水平および垂直の漸近線とも交差しません（手順5を参照）。前の手順で見つかった極値を除いて、チャートの方向を変更しないでください。
チップ
- 上記の手順を厳密に順番に実行した場合、ソリューションをテストするために2次導関数（または同様の複素数）を計算する必要はありません。
- 量の値を計算する必要がない場合は、座標のいくつかの追加のペアを計算することによって、局所的な極値を見つけることを置き換えることができます（NS, で）漸近線の各ペア間。さらに、説明されている方法がどのように機能するかを気にしない場合でも、導関数を見つけて方程式N '（NS） NS （NS） - NS （NS） NS '（NS) = 0.
- 場合によっては、高次の多項式を使用する必要があります。因数分解や数式などを使用して正確な解が見つからない場合は、ニュートン法などの数値法を使用して可能な解を推定します。
- まれに、分子と分母が共通の可変係数を共有します。説明されている手順によると、これにより、同じ場所でゼロと垂直方向の漸近線が生成されます。ただし、これは不可能であり、説明は次のいずれかです。
- Nのゼロ（NS）Dの多重度がゼロよりも高い（NS）。グラフF（NS）はこの時点でゼロになる傾向がありますが、そこでは定義されていません。ポイントの周りに円を描いてこれを示します。
- Nのゼロ（NS）およびDのゼロ（NS）同じ多重度を持っています。グラフは、この値でゼロ以外の点に近づいています NSしかし、そこでは定義されていません。ポイントの周りに円を描いてこれを示します。
- Nのゼロ（NS）Dの多重度がゼロよりも低い（NS）。ここに垂直方向の漸近線があります。
