二次方程式を因子に分析する - チップ

コンテンツ

手順
助言
あなたが必要なもの

数学では、 因子分析 与えられた数または方程式の積を持つ数または式を見つけることです。因子分析は、基本的な代数的問題を解決するために学ぶのに役立つスキルです。巧みに因数分解する能力は、作業に関してはほとんど重要です。代数方程式または他の多項式形式で。因子分析を使用して代数的表現を減らし、問題を単純化することができます。そのおかげで、手で解決するよりもはるかに速く特定の可能な答えを排除することさえできます。

手順

方法1/3：数値と基本的な代数表現を因子に分析する

単一の数値に適用する場合の因子分析の定義を理解します。 概念的には単純ですが、実際には、複雑な方程式を適用することは非常に困難な場合があります。したがって、最も簡単な因子分析の概念的アプローチは、単一の数値から始めて、より高度なアプリケーションに進む前に単純な方程式に進むことです。因子与えられた数は、同じ数の積を持つ数です。たとえば、1×12、2×6、および3×4はすべて12に等しいため、1、12、2、6、3、および4は12の係数です。
- 言い換えれば、与えられた数の要因は数です 分割されます その数で。
- あなたは60の完全な係数を見つけることができますか？ 60という数字は、多くの数字で割り切れるため、さまざまな目的（1時間の分、1分の秒など）で使用されます。
  - 数値60には、1、2、3、4、5、6、10、12、15、20、30、および60の要素があります。
変数を含む式も因数分解できることを理解してください。 独立した数値だけでなく、算術係数を持つ変数も因数分解できます。これを行うには、変数の係数の要因を見つける必要があります。分析を因数分解する方法を知ることは、変数を含む代数方程式を単純に変換するのに非常に役立ちます。
- たとえば、12xは、12とxの結果になるように書き換えることができます。 12xを3（4x）、2（6x）などと記述し、12の使用目的に最も適した要素を使用することができます。
  - あなたも12倍の分析に行くことができます 何度も。つまり、3（4x）または2（6x）で停止する必要はありません。4xと6xを分析して、それぞれ3（2（2x）2（3（2x））を取得できます。この式は同等です。
乗算の連想特性を適用して、代数方程式を因数分解します。 独立した数と係数の両方を因子に分析する知識を使用して、方程式に含まれる数と変数の共通の因子を見つけることにより、単純な代数方程式を単純化できます。多くの場合、方程式をできるだけ単純にするために、最大の一般的な除数を見つけようとします。この単純な変換は、乗算の連想性のおかげで可能です-すべての数値a、b、およびcについて、次のようになります。 a（b + c）= ab + ac.
- 次の問題の例を考えてみましょう。代数方程式12x + 6を因数分解するために、最初に、12xと6の最大の共通除算器を見つけます。6は12xと6の両方が割り切れる最大の数なので、簡単に変換できます。方程式を6（2x + 1）に減らします。
- 同じことが負の符号と分数を持つ方程式にも当てはまります。たとえば、x / 2 + 4は単純に1/2（x + 8）に変換でき、-7x + -21は-7（x + 3）に分解できます。
広告

方法2/3：二次方程式の因子への分析

方程式が2次形式（ax + bx + c = 0）であることを確認してください。 二次方程式の形式はax + bx + c = 0です。ここで、a、b、およびcは定数であり、aは非ゼロです（a 五月 1または-1に等しい）。 1変数（x）方程式にxの2乗を含む1つ以上の項が含まれている場合、通常、等符号の片側の基本的な代数演算子を0に変換し、axなどを使用できます。反対側に。
- たとえば、代数方程式5x + 7x-9 = 4x + x-18は、2次形式であるx + 6x + 9 = 0に減らすことができます。
- x、xなど、xの指数が高い方程式。二次にすることはできません。 xの3乗以上を含む項を削除して方程式を減らすことができない限り、それらは2次、4次、...です。
二次方程式では、a = 1の場合、（x + d）（x + e）に分解されます。ここで、d×e = cおよびd + e = bです。 二次方程式がx + bx + c = 0の形式である場合（つまり、x = 1の係数の場合）、比較的高速な計算を使用できる可能性があります（ただし確実ではありません）。この方程式を因数分解するのは簡単です。 cに等しい2つの数値を見つける そして 合計はbに等しい。 dとeを見つけたら、次の式に置き換えます。 （x + d）（x + e）。これらの2つの要素を掛け合わせると、上記の2次方程式が得られます。つまり、これらは方程式の要素です。
- たとえば、2次方程式x + 5x + 6 = 0を考えます。3と2は6の積を持ち、同時に合計5を持ちます。したがって、方程式を（x + 3）（に簡単に変換できます。 x + 2）。
- 方程式自体が少し異なる場合、この基本的なクイックフィックスは少し異なります。
  - 二次方程式がx-bx + cの形式である場合、答えは次の形式になります：（x --_）（x --_）。
  - x + bx + cの形式の場合、答えは（x + _）（x + _）になります。
  - x-bx-cの場合、応答は（x + _）（x --_）の形式になります。
- 注：スペースには、分数または小数を含めることができます。たとえば、方程式x +（21/2）x + 5 = 0は（x + 10）（x + 1/2）に分解されます。
可能であれば、テストによって因子分析を実行します。 信じられないかもしれませんが、単純な2次方程式を使用すると、受け入れられる因数分解の方法の1つは、単に問題を調べて、考えられるすべての答えを次のようになるまで比較検討することです。正解。テスト方法とも呼ばれます。方程式の形式がax + bx + cでa> 1の場合、因数分解は（dx +/- _）（ex +/- _）の形式になります。ここで、dとeは定数です。もう一方はaと等しくありません。 dまたはe（または両方）五月 1に等しいが、必ずしもそうであるとは限らない。両方が1に等しい場合、基本的に上記のクイックワークを使用します。
- 次の問題の例を考えてみましょう。一見すると、3x-8x +4はかなり威圧的に見えます。ただし、3には2つの要素（3と1）しかないことに気付くと、答えは（3x +/- _）（x +/- _）の形式でなければならないことがわかっているため、問題は簡単になります。この場合、-2を両方のスペースに置き換えると正しい答えが得られます。 -2×3x = -6xおよび-2×x = -2x。 -6xと-2xの合計は-8xに等しい。 -2×-2 = 4であるため、括弧内に解析された要素が初期方程式を与えていることがわかります。
正方形を完成させて問題を解決します。 場合によっては、2次方程式は、特別な代数的アイデンティティを使用してすばやく簡単に乗算できます。 x + 2xh + h =（x + h）の形式の2次方程式。したがって、方程式でbがcの平方根の2倍である場合、方程式は（x +（sqrt（c）））に分解できます。
- たとえば、方程式x + 6x +9はこの形式に適合します。 3は9に等しく、3×2は6に等しいので、この方程式の因数分解形式は（x + 3）（x + 3）、または（x + 3）であることがわかります。
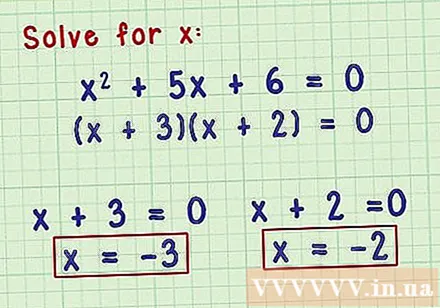
二次方程式を因子で解きます。 いずれにせよ、二次式が因数分解されたら、各因数をゼロにしてそれを解くことにより、xの値に対する可能な答えを見つけることができます。方程式がゼロになるようなxの値を探しているので、係数をゼロにするxは、その方程式の可能な解決策になります。
- 方程式x + 5x + 6 = 0に戻ります。これは（x + 3）（x + 2）= 0に分解されます。1つの係数がゼロの場合、方程式全体がゼロになります。 xの可能な解決策は、（x + 3）と（x + 2）をそれぞれ0、-3、-2に等しくする数です。
あなたの答えをチェックしてください-いくつかはエキゾチックかもしれません！ xの可能な解を見つけたら、それらを元の方程式に置き換えて、それらが正しいかどうかを判断します。時々、答えはそれを見つけます 問題ない 置き換えられると、元の方程式はゼロになります。これらのソリューションを エキゾチック そしてそれらを排除します。
- x + 5x + 6 = 0の場合は-2と-3を置き換えましょう。まず、-2：
  - (-2) + 5(-2) + 6 = 0
  - 4 + -10 + 6 = 0
  - 0 = 0。はい。したがって、-2は方程式の有効な解です。
- それでは、-3で試してみましょう。
  - (-3) + 5(-3) + 6 = 0
  - 9 + -15 + 6 = 0
  - 0 = 0。これも当てはまるため、-3も方程式の有効な解です。
広告

方法3/3：他のタイプの方程式を因子に分析する

方程式がa-b形式の場合は、（a + b）（a-b）に分解します。 分析された2変数方程式は、基本的な2次方程式とは異なります。 aとbがゼロ以外のa-b方程式は、（a + b）（a-b）に分解されます。
- たとえば、式9x-4y =（3x + 2y）（3x-2y）。
方程式がa + 2ab + bの形式である場合、それを（a + b）に分解します。 三項がaの形式である場合は注意してください-2ab + b、因数分解形式はわずかに異なります：（a-b）。
- 式4x + 8xy + 4yは、4x +（2×2×2）xy + 4yと書き直すことができます。これで、正しい形式であることがわかり、この方程式の因数分解形式は（2x + 2y）であると自信を持って言えます。
方程式がa-b形式の場合は、それを（a-b）（a + ab + b）に分解します。 最後に、3次方程式やさらに高次の方程式を因数分解できると言わなければなりません。ただし、分析プロセスはすぐに非常に複雑になります。
- たとえば、8x-27yは（2x-3y）（4x +（（2x）（3y））+ 9y）に分解されます
広告

助言

a-bは因数分解できますが、a + bは因数分解できません。
定数を因数分解する方法を覚えておいてください-それは役に立つかもしれません。
因数分解の過程で分数に注意を払い、それらを正しく適切に処理します。
x + bx +（b / 2）トライデントの場合、その因数分解は（x +（b / 2））になります（正方形を完成させているときにこの状況に遭遇する可能性があります）。
a0 = 0（プロパティにゼロを掛けたもの）であることを忘れないでください。