コンテンツ

• ステップに
• 2の方法1/2：方法1：クロス乗算
• 2の方法2：方法2：分母の最小公倍数（LCM）を見つける
• チップ

有理関数は、分子または分母に1つ以上の変数がある分数です。有理方程式は、少なくとも1つの有理式を含む方程式です。一般的な代数方程式と同様に、変数が等号の片側に分離されるまで、方程式の両側に同じ演算を適用することにより、有理式を解くことができます。帰一算と分母の最小公倍数を見つけるという2つの特別な方法は、変数の分離と有理方程式の解法に特に役立ちます。

ステップに

2の方法1/2：方法1：クロス乗算

1. 必要に応じて、等号の両側に分数があることを確認するために方程式を再配置します。 クロス乗算は、有理方程式を解くための高速な方法です。残念ながら、この方法は、等号の両側に1つの有理式または分数がある有理方程式に対してのみ機能します。これが方程式に当てはまらない場合は、項を適切な場所に配置するために、おそらく代数演算が必要になります。
   • たとえば、方程式（x + 3）/ 4-x /（-2）= 0は、方程式のいずれかの側にx /（-2）を加算することにより、正しい帰一算形式に簡単に変換できます。次のようになります：（x + 3）/ 4 = x /（-2）。
     • 小数と整数は、分母1を指定することで、分数に変換できることに注意してください。たとえば、（x + 3）/ 4-2.5 = 5は、（x + 3）/ 4 = 7.5 / 1と書き直すことができます。これにより、クロス乗算を適用できます。
   • 一部の有理方程式は、簡単に正しい形式に変換できません。そのような場合は、最小公倍数の分母を使用する方法を使用してください。
2. クロス乗算。 クロス乗算とは、単に一方の分数の分子にもう一方の分母を乗算すること、またはその逆を意味します。等号の左側の分数の分子に右側の分数を掛けます。右側の分子と左側の分母で繰り返します。
   • クロス乗算は、一般的な代数的原理に従って機能します。有理式やその他の分数は、分母を掛けることで通常の数に変換できます。基本的に、クロス乗算は、方程式の両辺に分数の両方の分母を乗算する便利な簡略化された方法です。信じられませんか？試してみてください。単純化しても同じ結果が表示されます。
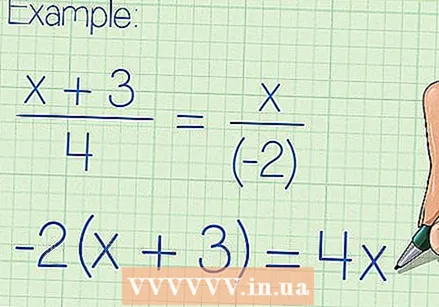3. 2つの製品を互いに等しくします。 クロス乗算の後、2つの積が残ります。これらの2つの項を等しくし、それらを単純化して、方程式の両側で最も単純な項を取得します。
   • たとえば、（x + 3）/ 4 = x /（-2）が元の有理式である場合、帰一算後は-2（x + 3）= 4xに等しくなります。これは、オプションで-2x-6 = 4xと書き直すことができます。
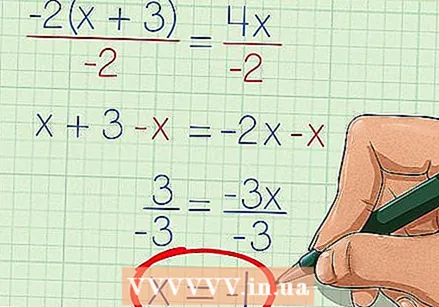4. 変数を解きます。 代数演算を使用して、方程式内の変数の値を見つけます。 xが等号の両側に表示される場合は、x項を加算または減算して、等号の片側にx項しかないことを確認してください。
   • この例では、方程式の両辺を-2で除算することができます。これにより、x + 3 = -2xが得られます。等号の両側からxを引くと、3 = -3xになります。そして最後に、両側を-3で割ると、-1 = x、またはx = -1になります。これで、有理方程式を解くxが見つかりました。

2の方法2：方法2：分母の最小公倍数（LCM）を見つける

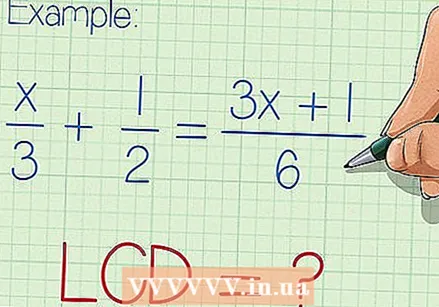1. 最小公倍数の分母を見つけるのは明らかです。 分母の最小公倍数（LCM）は、有理式の簡略化に使用でき、変数の値を見つけることができます。等号の両側に分数または有理式が1つしかない形式に有理方程式を簡単に書き直すことができない場合は、LCMを見つけることをお勧めします。 3項以上の有理方程式を解くには、LCMが便利なツールです。しかし、2つの項しかない有理方程式を解く場合、多くの場合、帰一算の方が高速です。
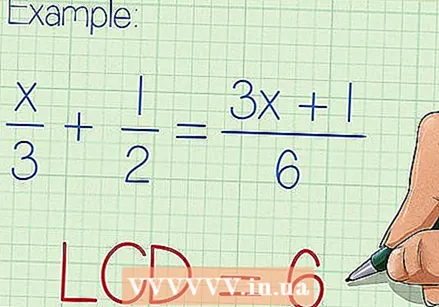2. 各分数の分母を調べます。 分母で完全に割り切れる最小の数を見つけます。これはあなたの方程式のLCMです。
   • 最小公倍数（各分母で完全に割り切れる最小の数）がすぐに明らかになる場合があります。たとえば、式がx / 3 + 1/2 =（3x + 1）/ 6のように見える場合、LCMは3、2、および6で割り切れ、したがって6に等しくなければならないことが簡単にわかります。
   • しかし、多くの場合、合理的な比較のLCMはすぐにはまったく明確ではありません。そのような場合は、他の小さい分母の倍数を含む数が見つかるまで、最大の分母の倍数を試してください。多くの場合、LCMは2つの分母の積です。たとえば、方程式x / 8 + 2/6 =（x-3）/ 9を考えます。ここで、LCMは8 * 9 = 72に等しくなります。
   • 1つ以上の分母に変数が含まれている場合、このプロセスはやや困難になりますが、決して不可能ではありません。このような場合、LCMは、単一の数値だけでなく、すべての分母に完全に適合する式（変数を含む）です。例として、方程式5 /（x-1）= 1 / x + 2 /（3x）、ここでLCMは3x（x-1）に等しくなります。これは、分母で完全に割り切れるためです-（x-1で除算） ）は3xを生成し、3xで除算すると（x-1）が生成され、xで除算すると3（x-1）が生成されます。
3. 有理方程式の各分数に1を掛けます。 各項に1を掛けるのは役に立たないように思えるかもしれませんが、ここにはトリックがあります。つまり、1は分数として書くことができます-たとえば、2/2と3/3。有理方程式の各分数に1を掛け、各分母を掛けた数または項として毎回1を書き込んで、LCMを分数として求めます。
   • この例では、x / 3に2/2を掛けて2x / 6を取得し、1/2に3/3を掛けて3/6を取得できます。 3x +1/6にはすでに分母として6（lcm）があるので、1/1を掛けるか、そのままにしておくことができます。
   • 分母に変数があるこの例では、プロセス全体が少し複雑になっています。 LCMは3x（x-1）に等しいので、各有理式に分母として3x（x-1）を生成する分数を掛けます。 5 /（x-1）に（3x）/（3x）を掛けると、5（3x）/（3x）（x-1）になり、1 / xに3（x-1）/ 3（x -1）これにより3（x-1）/ 3x（x-1）が得られ、2 /（3x）に（x-1）/（x-1）を掛けると、最終的に2（x-1）/が得られます。 3x（x-1）。
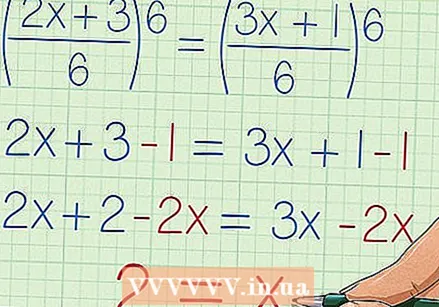4. xを単純化して解きます。 有理方程式のすべての項が同じ分母を持っているので、方程式から分母を削除して分子を解くことができます。方程式の両辺にLCMを掛けるだけで分母がなくなり、分子だけが残ります。これで、等号の片側で変数を分離することにより、変数を解くことができる通常の方程式になりました。
   • この例では、乗算後、1を分数として使用すると、2x / 6 + 3/6 =（3x + 1）/ 6が得られます。分母が同じ場合は2つの分数を追加できるため、この式は値を変更せずに（2x + 3）/ 6 =（3x + 1）/ 6と書くことができます。両側に6を掛けて分母をキャンセルし、2x + 3 = 3x +1を残します。ここでは、両側から1を引いて2x + 2 = 3xを残し、両側から2xを引いて2 = xを残します。これは、x = 2と書くこともできます。
   • 分母に変数があるこの例では、各項に「1」を掛けた後の方程式は、5（3x）/（3x）（x-1）= 3（x-​​1）/ 3x（x-1）+ 2（ x-1）/ 3x（x-1）。各項にLCMを掛けると、分母をキャンセルすることができます。これにより、5（3x）= 3（x-​​1）+ 2（x-1）が得られます。さらに詳しく説明すると、これは15x = 3x-3 + 2x -2になり、15x = x-5として再度簡略化できます。両側からxを引くと、14x = -5になるため、最終的な答えはx =-に簡略化できます。 5/14。

チップ

• 変数の値を見つけたら、元の方程式にこの値を入力して答えを確認します。変数の値を正しく取得すると、方程式を1 = 1などの単純で正しい定理に単純化できるはずです。
• すべての方程式は有理式として書くことができます。分母1の上に分子として配置するだけです。したがって、方程式x + 3は（x + 3）/ 1と書くことができ、どちらも同じ値になります。