三角方程式を解く

コンテンツ

ステップに

三角方程式は、可変三角曲線xの1つまたは複数の三角関数を持つ方程式です。 xを解くことは、三角関数が三角方程式を真にする三角曲線の値を見つけることを意味します。

解曲線の回答または値は、度またはラジアンで表されます。例：

x = Pi / 3; x = 5Pi / 6; x = 3Pi / 2; x = 45度; x = 37.12度; x = 178.37度

注：単位円では、任意の曲線の三角関数は、対応する角度の三角関数と同じです。単位円は、可変曲線xのすべての三角関数を定義します。また、基本的な三角方程式や不等式を解く際の証明としても使用されます。
三角方程式の例：
- sin x + sin 2x = 1/2; tan x + cot x = 1.732;
- cos 3x + sin 2x = cos x; 2sin 2x + cos x = 1。

単位円。
- これは、半径= 1の円です。ここで、Oは原点です。単位円は、可変曲線xの4つの主要な三角関数を定義し、反時計回りに円を描きます。
- 値xの曲線が単位円上で変化する場合、次のようになります。
- 横軸OAxは、三角関数f（x）= cosxを定義します。
- 縦軸OByは、三角関数f（x）= sinxを定義します。
- 縦軸ATは、三角関数f（x）= tanxを定義します。
- 横軸BUは、三角関数f（x）= cotxを定義します。

単位円は、円上の曲線xのさまざまな位置を考慮して、基本的な三角方程式と標準的な三角不等式を解くためにも使用されます。

ステップに

解決方法を理解します。
- 三角方程式を解くには、それを1つ以上の基本的な三角方程式に変換します。三角方程式を解くと、最終的に4つの基本的な三角方程式が解かれます。
基本的な三角方程式を解く方法を知っています。
- 4つの基本的な三角方程式があります。
- sin x = a; cos x = a
- tan x = a; cot x = a
- 基本的な三角方程式を解くには、三角円上の曲線xのさまざまな位置を調べ、三角変換テーブル（または計算機）を使用します。これらおよび同様の基本的な三角方程式を解く方法を完全に理解するには、次の本を読んでください：「三角法：三角方程式と不等式の解き方」（AmazonE-book 2010）。
- 例1.sin x = 0.866を解きます。変換テーブル（または計算機）は答えを与えます：x = Pi / 3。三角関数の円は、正弦（0.866）と同じ値を持つ別の曲線（2Pi / 3）を示します。三角関数の円は、拡張回答と呼ばれる無限の回答も提供します。
- x1 = Pi / 3 + 2k.Pi、およびx2 = 2Pi / 3。（期間内に返信（0、2Pi））
- x1 = Pi / 3 + 2k Pi、およびx2 = 2Pi / 3 + 2kPi。（詳細な回答）。
- 例2.解く：cos x = -1 / 2。電卓はx = 2 Pi / 3を与えます。三角関数の円もx = -2Pi / 3を与えます。
- x1 = 2Pi / 3 + 2k.Pi、およびx2 = -2Pi / 3。（期間（0、2Pi）の回答）
- x1 = 2Pi / 3 + 2k Pi、およびx2 = -2Pi / 3 + 2k.Pi. （拡張回答）
- 例3.解く：tan（x --Pi / 4）= 0。
- x = Pi / 4; （回答）
- x = Pi / 4 + k Pi; （拡張回答）
- 例4.解く：cot 2x = 1.732。電卓と三角関数の円は次のようになります。
- x = Pi / 12; （回答）
- x = Pi / 12 + k Pi; （拡張回答）
三角方程式を解く際に使用される変換について学びます。
- 特定の三角方程式を標準の三角方程式に変換するには、標準の代数変換（因数分解、共通因子、多項式など）、三角関数の定義とプロパティ、および三角アイデンティティを使用します。約31、14があり、そのうち19から31までは三角関数公式であり、三角方程式の変換に使用されるため、変換アイデンティティとも呼ばれます。上記の本を参照してください。
- 例5：三角方程式：sin x + sin 2x + sin 3x = 0は、三角関数公式を使用して基本的な三角方程式の積に変換できます：4cos x * sin（3x / 2） * cos（x / 2）= 0.解くべき基本的な三角方程式は次のとおりです。cosx= 0; sin（3x / 2）= 0;およびcos（x / 2）= 0。
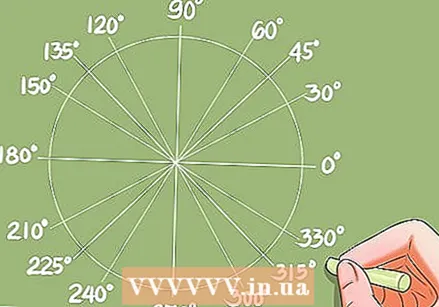三角関数がわかっている曲線を見つけます。
- 三角方程式を解く方法を学ぶ前に、三角関数がわかっている曲線をすばやく見つける方法を知る必要があります。曲線（または角度）の変換値は、三角関数表または計算機を使用して決定できます。
- 例：cos x = 0.732を解きます。電卓は解x = 42.95度を与えます。単位円は、コサインに同じ値を持つ他の曲線を示します。
単位円上に答えの弧を描きます。
- グラフを作成して、単位円上の解を示すことができます。これらの曲線の終点は、三角関数の円上の正多角形です。いくつかの例：
- 曲線の端点x = Pi / 3 +k。Pi/ 2は、単位円上の正方形です。
- x = Pi / 4 + k.Pi / 3の曲線は、単位円上の六角形の座標で表されます。
三角方程式を解く方法を学びます。
- 与えられた三角方程式に三角関数が1つしかない場合は、それを標準の三角方程式として解きます。与えられた方程式に2つ以上の三角関数が含まれている場合、方程式を変換するためのオプションに応じて、2つの解法があります。
  - A.方法1。
- 三角方程式を次の形式の積に変換します：f（x）.g（x）= 0またはf（x）.g（x）.h（x）= 0、ここでf（x）、g（x）およびh（x）は基本的な三角方程式です。
- 例6.解く：2cos x + sin 2x = 0。（0 x 2Pi）
- 解決。次の恒等式を使用して、方程式のsin2xを置き換えます。sin2x= 2 * sin x * cosx。
- cos x + 2 * sin x * cos x = 2cos x *（sin x + 1）= 0。次に、2つの標準三角関数cos x = 0と（sin x + 1）= 0を解きます。
- 例7.解く：cos x + cos 2x + cos 3x = 0。（0 x 2Pi）
- 解決策：三角関数の恒等式cos 2x（2cos x + 1）= 0を使用して、これを積に変換します。次に、2つの基本的な三角方程式を解きます：cos 2x = 0、および（2cos x + 1）= 0。
- 例8.解く：sin x --sin 3x = cos2x。（0 x 2Pi）
- 解決策：三角関数の恒等式を使用して、これを積に変換します：-cos 2x *（2sin x + 1）= 0。次に、2つの基本的な三角方程式を解きます：cos 2x = 0、および（2sin x + 1）= 0。
  - B.アプローチ2。
- 三角方程式を、変数として1つの一意の三角関数のみを持つ三角方程式に変換します。適切な変数を選択する方法に関するヒントがいくつかあります。一般的な変数は次のとおりです。sinx= t; cos x = t; cos 2x = t、tan x = tおよびtan（x / 2）= t。
- 例9.解く：3sin ^ 2 x-2cos ^ 2 x = 4sin x + 7（0 x 2Pi）。
- 解決。方程式で、（cos ^ 2x）を（1-sin ^ 2x）に置き換え、方程式を単純化します。
- 3sin ^ 2 x-2 + 2sin ^ 2 x-4sin x-7 = 0。ここで、sin x = tを使用します。方程式は次のようになります。5t^ 2-4t-9 = 0。これは、t1 = -1とt2 = 9/5の2つの根を持つ2次方程式です。 > 1であるため、2番目のt2を拒否できます。t= sin = -1-> x = 3Pi / 2を解きます。
- 例10.解く：tan x + 2 tan ^ 2 x = cot x +2。
- 解決。 tan x = tを使用します。与えられた方程式を変数としてtを持つ方程式に変換します：（2t + 1）（t ^ 2 --1）= 0。この積からtを解き、次に標準の三角方程式tan x = t forxを解きます。
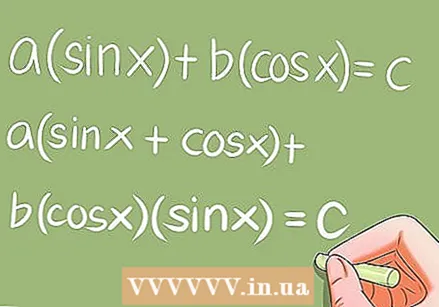特別な三角方程式を解きます。
- いくつかの特定の変換を必要とするいくつかの特別な三角方程式があります。例：
- a * sin x + b * cos x = c; a（sin x + cos x）+ b * cos x * sin x = c;
- a * sin ^ 2 x + b * sin x * cos x + c * cos ^ 2 x = 0
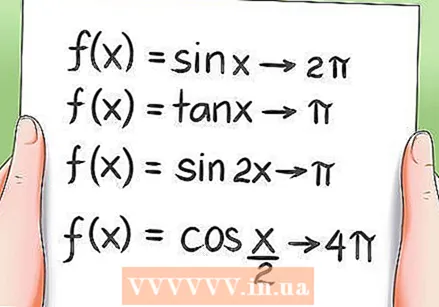三角関数の周期特性を学びます。
- すべての三角関数は周期的です。つまり、一定期間回転した後、同じ値に戻ります。例：
  - 関数f（x）= sin xは、周期として2Piを持ちます。
  - 関数f（x）= tan xは、円周率として円周率を持ちます。
  - 関数f（x）= sin 2xは、周期として円周率を持ちます。
  - 関数f（x）= cos（x / 2）は、周期として4Piを持ちます。
- 演習/テストで期間が指定されている場合は、この期間内の曲線xを見つける必要があります。
- 注：三角方程式を解くのは難しいため、エラーや間違いにつながることがよくあります。したがって、回答は慎重に確認する必要があります。解いた後、グラフ電卓を使用して答えを確認し、与えられた三角方程式R（x）= 0を直接表すことができます。答え（平方根として）は小数点以下の桁数で示されます。例として、Piの値は3.14です。