コンテンツ

• ステップに
• パート1/3：分析の基本
• パート2/3：デリバティブを理解する
• パート3/3：積分を理解する
• チップ

分析（微積分とも呼ばれます）は、極限、関数、導関数、積分、および無限級数に焦点を当てた数学の一分野です。この主題は多くの数学をカバーし、物理学と力学で使用される公式と方程式の多くの根底にあります。分析を正しく理解するには、高校で数年の数学が必要になる可能性がありますが、この記事では、重要な概念を認識し、理論をよりよく理解する方法を学びます。

ステップに

パート1/3：分析の基本

1. 分析は、物事がどのように変化するかを研究することです。 分析は、通常は実世界のデータから取得された数値とグラフを調べ、それらがどのように変化するかを説明する数学の一分野です。これは最初はあまり役に立たないように思われるかもしれませんが、分析は数学で最も一般的に使用される分野の1つです。ある時点でビジネスがどれだけ速く成長しているか、宇宙船の進路をグラフ化する方法、燃料がどれだけ早く使い果たされているかを示すツールがあると想像してみてください。分析は、工学、経済学、統計学、化学、物理学の重要なツールであり、多くの発明や発見に貢献してきました。
2. 関数は2つの数値間の関係であり、関係のマッピングに使用されます。 それらは数の関係のルールであり、数学者はそれらを使用してグラフを作成します。関数では、各入力の結果は1つだけです。例： ${ displaystyle y = 2x + 4、}$無限の概念について考えてください。 無限大は、プロセスの絶え間ない繰り返しです。それは特定の場所ではなく（無限に行くことはできません）、永遠に行われた場合の数値または方程式の動作です。これは変化を研究するために重要です。ある時点での車の動きの速さを知りたい場合がありますが、それは現在の1秒間の車の動きの速さですか。ミリ秒？ナノ秒？無限に小さい時間のチャンクをさらに正確に見つけることができます。それが分析の出番です。
3. 制限の概念を理解します。 制限は、何かが無限に近づくと何が起こるかを示します。数1を取り、それを2で割ります。2で何度も割り続けます。 1は1/2になり、次に1 / 4、1 / 8、1 / 16、1 / 32などになります。数値がどんどん小さくなるたびに、ゼロに「近く」なります。しかし、それはどこで止まりますか？ゼロにするために1を2で割る必要があるのは何回ですか？この質問に答える代わりに、分析では1つを設定します 制限 この場合、制限はです。
   • 制限はグラフで視覚化するのが最も簡単です。たとえば、グラフがほとんど触れているが、完全には触れていないポイントはありますか？
   • 制限は、数、無限、または存在しない場合があります。たとえば、加算シーケンス1 + 2 + 2 + 2 + 2 + ...を使用すると、これが無期限に続くと、最終的な数は無限に大きくなります。その後、制限は無限になります。
4. 代数、三角法、および数学の基礎の基本的な数学の概念を確認します。 分析は、あなたが以前に学んだ数学の多くに依存しています。すべてのトピックについて十分な情報を得ていると、分析の学習と理解がはるかに簡単になります。ブラッシュアップするいくつかのトピックは次のとおりです。
   • 代数。さまざまなプロセスを理解し、複数の変数を使用して方程式や連立方程式を解くことができる必要があります。コレクションの基本を理解します。グラフの作成を練習します。
   • ジオメトリ。幾何学は形の研究です。三角形、長方形、円、および周囲長や面積などの計算方法に関する基本的な知識が必要です。角度、線、座標を理解する
   • 三角法。三角法は、円と直角三角形の特性を扱う数学の一分野です。三角関数のアイデンティティ、グラフ、関数、および逆三角関数の使用方法を理解します。
5. グラフ電卓を購入します。 分析は、あなたが何をしているのかを見ずに理解するのは簡単ではありません。グラフ電卓は関数を視覚化するので、扱っている方程式をよりよく理解できます。多くの場合、制限は画面にも表示され、導関数と関数は自動的に計算されます。
   • 今日の多くのスマートフォンやタブレットは、グラフ電卓を購入したくない、または購入できない場合に、安価で効果的なグラフアプリを提供しています。

パート2/3：デリバティブを理解する

1. 分析は、「特定の瞬間の変化」を研究するために使用されます。 正確な瞬間に何かが変化する理由を知ることは、分析の中核です。たとえば、分析により、車の速度だけでなく、その速度が任意の時点でどの程度変化するかもわかります。これは分析の最も簡単な使用法の1つですが、非常に重要です。宇宙船を月に到達させるのにかかる速度を決定する上で、そのような情報がどれほど重要であるか想像してみてください。
   • 特定の時点での変化を判断することは 差別化。分化は、分析の2つの主要な分野の最初のものです。
2. デリバティブを使用して、特定の時間に物事がどのように変化するかを理解します。 「派生語」は、学生をしばしば緊張させる何かの良い言葉です。ただし、概念自体はそれほど理解しにくいものではありません。つまり、「何かがどれだけ速く変化するか」という意味です。あなたが日常生活で最も遭遇する派生物はスピードと関係があります。ただし、通常は「速度の導関数」ではなく、単に「加速」と呼びます。
   • 加速は派生物です-何かが加速または減速している速度、またはその速度がどのように変化しているかを示します。
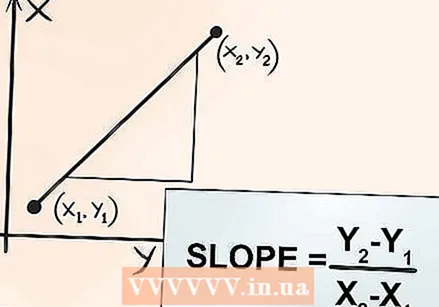3. 変化率が2点間の傾きに等しいことを知ってください。 これは、分析の最も重要な発見の1つです。 2点間の変化率は、これら2点間の線の傾きに等しくなります。方程式のような単純な線を考えてみてください 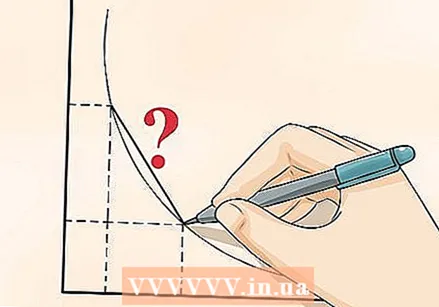${ displaystyle y = 3x。}$曲線の傾きを決定できることを知ってください。 直線の傾きを決定するのは比較的簡単です：どのくらいの変化 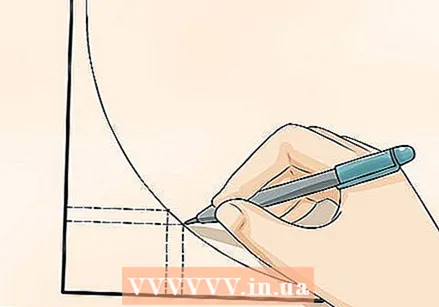${ displaystyle y}$変化をより正確に計算したい場合は、ポイントが互いに近くにあることを確認してください。 2つのポイントを近づけるほど、答えは正確になります。アクセルを踏んだときに車がどれだけ加速するかを知りたいとします。家とスーパーマーケットの間の速度の変化を測定したくはありませんが、アクセルを踏んだ瞬間からの速度の変化を測定したいと思います。読み取り値がその一瞬に近づくほど、変化の計算がより正確になります。
   • たとえば、科学者たちは、いくつかの種を救うためにどれだけ早く絶滅するかを調査しています。ただし、夏よりも冬に死亡する動物の数が多いため、年間の変化率を調べることは有用ではありません。7月1日から8月1日までなど、より短い期間で変化率を決定することをお勧めします。
4. 無限に短い線を使用して、「瞬間的な変化率」を決定するか、導関数を見つけます。 これは分析が少し混乱することが多いところですが、これは実際には2つの単純な事実の結果です。まず第一に、あなたは線の傾きがその線がどれだけ速く変化するかに等しいことを知っています。次に、線のポイントが互いに近いほど、読み取りがより正確になることがわかります。しかし、勾配が2つのポイント間の関係である場合、特定のポイントでの変化率をどのように見つけますか？答え： 互いに無限に近い2つのポイントを選択します.
   • 1を2で割り続けて、1 / 2、1 / 4、1 / 8などになる例を考えてみましょう。つまり、最終的にはゼロに近づき、答えは「ほぼゼロ」になります。ポイントは互いに非常に接近しているため、「ほぼ等しい」。これがデリバティブの性質です。
5. さまざまなデリバティブを決定する方法を学びます。 方程式に応じて導関数を見つけるためのさまざまな手法がたくさんありますが、上記の導関数の基本を覚えていれば、それらのほとんどは理にかなっています。すべての導関数は、「微小」線の傾きを見つける方法です。微分理論についてもっと知ったので、仕事の多くは答えを見つけることです。
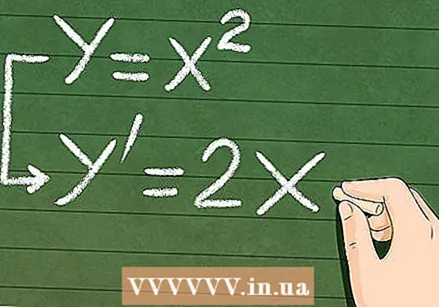6. 導出された方程式を見つけて、いつでも変化率を予測します。 導関数を使用して任意の時点での変化率を決定することは有用ですが、分析の利点は、任意の関数の新しいモデルを作成できることです。の導関数 ${ displaystyle y = x ^ {2}、}$これを理解するのが難しい場合は、デリバティブの実際の例を覚えておいてください。 最も単純な例は速度​​に基づいており、これには私たちが毎日遭遇するさまざまな派生物が含まれます。忘れてはいけない： 導関数は、何かがどれだけ速く変化するかの尺度です。簡単な実験を考えてみてください。あなたはテーブルの上で大理石を転がし、それがどれだけ遠くに移動し、どれだけ速く動くかを毎回測定します。ここで、回転するビー玉がグラフ上の線をたどると想像してください。導関数を使用して、その線上の任意の時点での瞬間的な変化を測定しています。
   • 大理石はどれくらい速く動きますか？動く大理石の位置（または派生物）はどのくらいの速度で変化しますか？この導関数を「速度」と呼びます。
   • 大理石を斜面に沿って転がし、速度がどのように変化するかを観察します。大理石の速度の変化率、または導関数はどれくらいですか？この導関数は、私たちが「加速」と呼ぶものです。
   • ジェットコースターなどの波状のトラックに沿って大理石を転がします。ビー玉が転がるとき、ビー玉はどの程度速度を上げますか？また、ビー玉は上り坂でどの程度遅くなりますか？大理石が最初の丘の途中にあるとき、大理石は正確にどのくらいの速さで進みますか？これは、その特定のポイントでのその大理石の瞬間的な変化率または導関数です。

パート3/3：積分を理解する

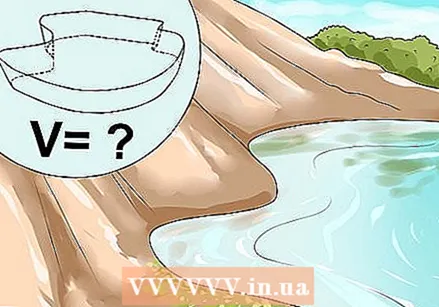1. 分析を使用して、複雑な領域とボリュームを見つけることができることを知ってください。 分析を使用すると、他の方法では測定が難しい複雑な形状を測定できます。たとえば、長くて不規則な形の湖に含まれる水量を知りたいという問題を考えてみましょう。1リットルの水を個別に測定したり、定規を使用して湖の形を測定したりすることは不可能です。分析を使用すると、湖の端がどのように変化しているかを調べ、その情報を使用して、湖に含まれる水量を調べることができます。
   • 幾何学的モデルの作成と体積の研究 統合する。統合微積分は、分析の2番目に重要な分野です。
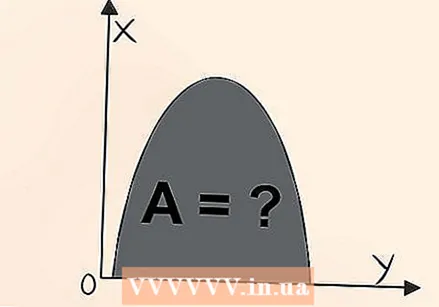2. 統合はグラフの下の領域であることを知ってください。 統合は、線の下のスペースを測定するために使用されます。これにより、奇妙な形状または不規則な形状の領域を決定できます。方程式を取る 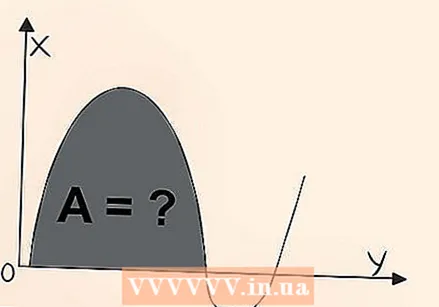${ displaystyle y = 4-x ^ {2}、}$統合する領域を選択する必要があることを知ってください。 関数全体を単純に統合することはできません。例えば、 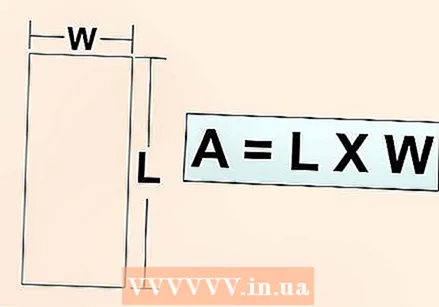${ displaystyle y = x}$長方形の面積を計算する方法を考えてください。 グラフの上に次のような平らな線があるとします。 ${ displaystyle y = 4.}$積分計算では、領域の領域を見つけるために多くの小さな長方形が一緒に追加されることを知っています。 曲線を大きく拡大すると、直線のように見えます。あなたはこれを毎日見ます-あなたは地球の表面にとても近いのであなたは地球の曲率を知覚することができません。統合により、曲線の下に無限の数の小さな長方形が作成されます。これらの長方形は非常に小さいため、基本的に平坦であるため、数えることができます。一緒に追加されたこれらすべての長方形は、曲線の下の領域の領域を形成します。
   • グラフの下にたくさんの小さなセグメントを合計すると、それが各セグメントの幅になります。 ほとんど はゼロです。
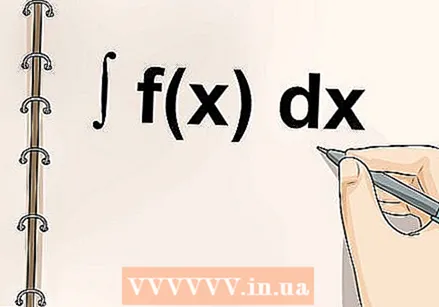3. 積分を正しく読み書きする方法を知っている。 積分は4つの部分で構成されています。典型的な積分は次のようになります。
   
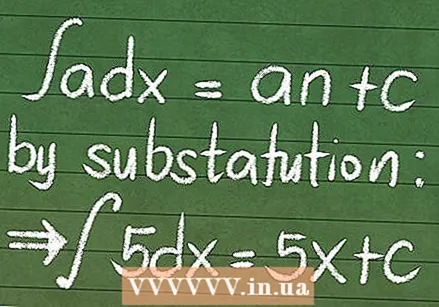   ${ displaystyle int f（x） mathrm {d} x}$ 積分を見つけることについてもっと学ぶ. 統合にはさまざまな形式があり、各関数を統合するにはさまざまな式を学ぶ必要があります。ただし、それらはすべて上記の原則に従います。統合とは、無限の数の合計です。
   • 置換によって統合します。
   • 不定積分を計算します。
   • 共有して統合します。
4. 統合は差別化の逆であり、その逆であることを知ってください。 これは分析の経験則であり、非常に重要であるため、独自の名前が付けられています。それは、積分計算の主定理です。統合と微分は非常に密接に関連しているため、2つの組み合わせを使用して、情報の種類に関係なく、変化率、加速度、速度、位置、動きなどを決定できます。
   • たとえば、速度の導関数は加速度であるため、速度を使用して加速度を見つけることができます。しかし、何か（重力によって落下する物体など）の加速度しかわからない場合は、統合して速度を取り戻すことができます。
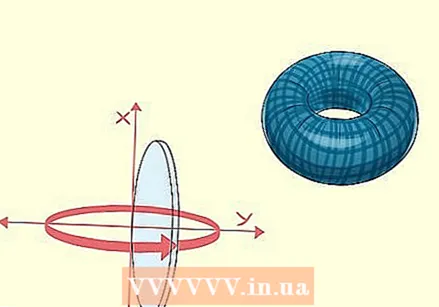5. 統合により、3Dオブジェクトのボリュームも制御できることを理解してください。 平らな形状を回転させることは、3Dソリッドを作成する1つの方法です。テーブルの上でコインが回転しているところを想像してみてください。コインが回転すると球の形をしているように見えることに注目してください。この概念により、「回転によるボリューム」と呼ばれるプロセスに従ってボリュームを決定できます。
   • これにより、それを表す関数がある限り、任意の固体の体積を決定できます。たとえば、湖の底を追跡する関数を作成し、それを使用して湖の体積や湖に含まれる水の量を決定できます。

チップ

• 練習は完璧になるので、教科書の練習問題（先生が教えていないものでも）を行い、答えを確認して、概念をよりよく理解するのに役立ててください。
• 解決策が見つからない場合は、先生に聞いてください。